如何在 Google 表格中舍入數字
在這篇文章中,我們將向您展示如何在 Google 表格中對數字進行四捨五入。電子表格數據通常由介於整數之間的小數組成。小數由小數點(或點)組成,小數點將整數與其小數部分分開。將數字四捨五入到某個小數位通常是個好主意,這樣可以更輕鬆地處理小數數據。四捨五入用於通過縮短小數點右側的位數來簡化數字。它還使數據看起來更均勻或對稱。在本文中,我們將向您展示如何使用七種不同的方法對 Google 表格中的數字進行四捨五入。
如何在 Google 表格中舍入數字
您可以使用以下方法對 Google 表格中的數字進行四捨五入:
- 使用 ROUND 函數對數字進行舍入。
- 使用 ROUNDUP 函數對數字進行舍入。
- 使用 ROUNDDOWN 函數對數字進行舍入。
- 使用 MROUND 函數對數字進行舍入。
- 使用 INT 函數對數字進行舍入。
- 使用 FLOOR 函數對數字進行舍入。
- 使用 CEILING 函數對數字進行舍入。
讓我們詳細了解這些方法中的每一種。
1] 使用 ROUND 函數對數字進行舍入
ROUND函數按照標準規則將數字四捨五入到特定的小數位數,如下所示:
- 如果四捨五入數字右邊的數字小於 5,則四捨五入數字保持不變(向下四捨五入)。
- 如果舍入數字右邊的數字大於或等於 5,則該數字增加 1(向上舍入)。
Round函數的語法是:
ROUND(value, [places])
- 其中value是指需要四捨五入的數字,並且
- [位數]是指數字應四捨五入到的小數位數。它是一個可選參數。如果用戶未指定,則取值零 (0)。
現在讓我們了解如何使用 ROUND 函數對 Google 表格中的數字進行舍入。
A]小數點右邊的數四捨五入
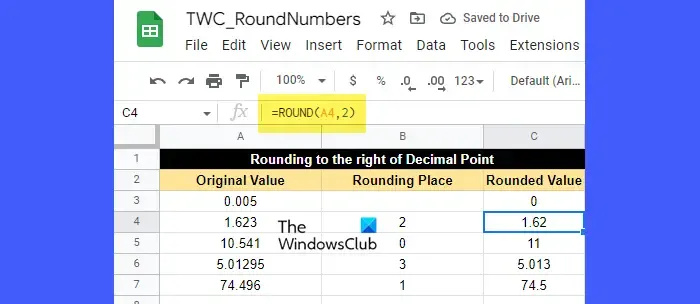
假設我們有一個電子表格,其中包含一些示例數據,如上圖所示。第一列列出了一些需要四捨五入到第二列中指定的位數的小數。要捨入這些數字,我們可以使用 ROUND 函數,如下所示:
將光標置於單元格 C3 中並鍵入以下函數:
=ROUND(A3)
由於單元格 A3 未指定數字需要四捨五入的小數位數,因此它將採用默認值 (0)。這意味著沒有四捨五入的數字,或者換句話說,該數字需要四捨五入到最接近的整數。現在由於小數點右邊的數字是0,小於5,所以小數點左邊的數字保持不變。因此結果值為 0,如單元格 C3 中所示。
對於下一個值(單元格 A4),四捨五入的位置是 2。因此需要將數字四捨五入到小數點後兩位。所以四捨五入的位數是2。四捨五入右邊的數字是3,小於5。所以四捨五入的位數將保持不變。因此,所得的四捨五入值為 1.62,如單元格 C4 中所示。
對於下一個值(單元格 A5),四捨五入位置為 0。同樣,該數字將四捨五入為最接近的整數,即 11,如單元格 C5 中所示。這裡,由於小數點右邊的數字等於 5,所以左邊的數字增加 1。
現在對於接下來的 2 個值(在單元格 A6 和 A7 中),您可以輕鬆確定 ROUND 函數如何舍入這些值。
B]小數點左邊的數字四捨五入
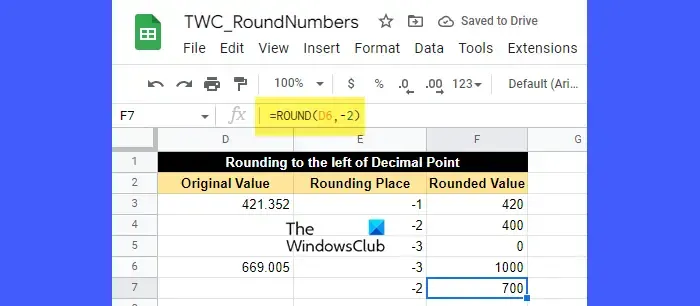
假設您需要將數字四捨五入到小數點左側而不是右側。為此,您需要在 places 參數中傳遞一個負值。
places 參數中的負值將刪除小數點右側的所有數字,並將小數點左側的數字舍入到最接近的十位、百位、千位等。
例如,請看上圖。我們在 ROUND 函數中傳遞了負值作為位置。這裡,
- -1 會將小數點左邊的數字四捨五入到最接近的十位。
- -2 會將小數點左邊的數字四捨五入到最接近的百位。
- -3 會將小數點左邊的數字四捨五入到最接近的千位,依此類推。
在此之後,單元格 D3 (421.352) 中的數字四捨五入到最接近的十位時變為 420,四捨五入到最接近的百位時變為 400,四捨五入到最接近的千位時變為 0。
同樣,單元格 D6 (669.005) 中的數字四捨五入到最接近的千位時變為 1000,四捨五入到最接近的百位時變為 700。
2] 使用 ROUNDUP 函數對數字進行舍入
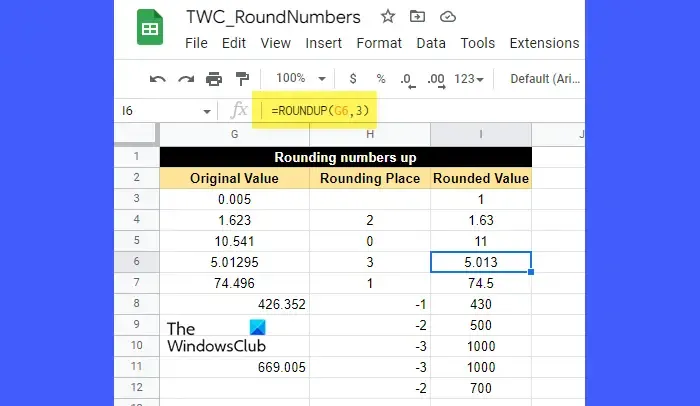
ROUNDUP函數的工作方式與 ROUND 函數類似,只是它總是向上舍入數字。ROUNDUP 函數的語法是:
ROUNDUP(value, [places])
- 其中value是需要向上舍入的數字,並且
- [位數]是指數字應四捨五入到的小數位數。它是一個可選參數,其默認值為零 (0)。如果在 places 參數中傳遞負值,則小數點左側的數字向上舍入。
現在看看上面的圖片。如您所見,所有數字都向上舍入到小數點右側或小數點左側的特定小數位,具體取決於 places 參數的值是正數還是負數。
例如,單元格 G4 (1.623) 中的值已四捨五入到小數點後兩位。這里四舍五入的地方是2,也就是第2位,2的下一位是3,也就是小於5。不過,由於這是一個ROUNDUP函數,結果的值將是1.63,而不是1.62。
同樣,單元格 G8 (426.352) 中的值在四捨五入到最接近的十位時變為 430(而不是 420)。
3] 使用 ROUNDDOWN 函數對數字進行舍入
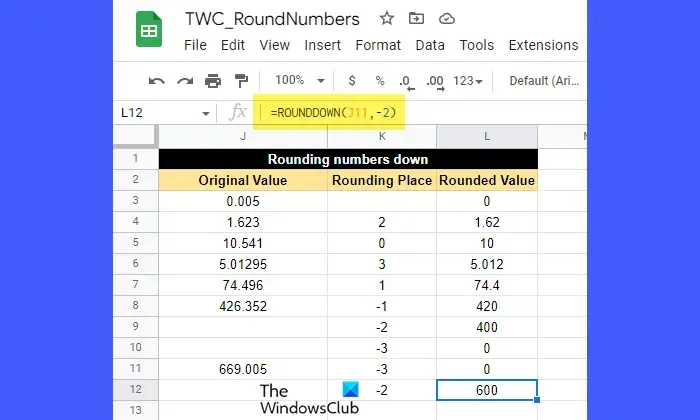
ROUNDDOWN函數也像 ROUND 函數一樣工作,只是它總是向下舍入數字。
ROUNDDOWN 函數的語法是:
ROUNDDOWN (value, [places])
- 其中value是需要向下舍入的數字,並且
- [位數]是指數字應四捨五入到的小數位數。它是一個可選參數,如果用戶未指定,則取值零 (0)。如果在 places 參數中傳遞負值,則小數點左側的數字向下舍入。
現在看看上面的圖片。看著這些數字,您可能很容易理解 ROUNDDOWN 函數如何將數字向下舍入到一定的小數位。根據 places 參數的值(正數或負數),將數字四捨五入到小數點右側或小數點左側。
例如,單元格 J7 (74.496) 中的值已向下舍入到小數點後一位。這里四舍五入的地方是 1,也就是數字 4。4 右邊的數字是 9,也就是大於 5。但是,四捨五入後的值將是 74.4 而不是 74.5,因為單元格已經應用了 ROUNDDOWN 函數價值。
4] 使用 MROUND 函數對數字進行舍入
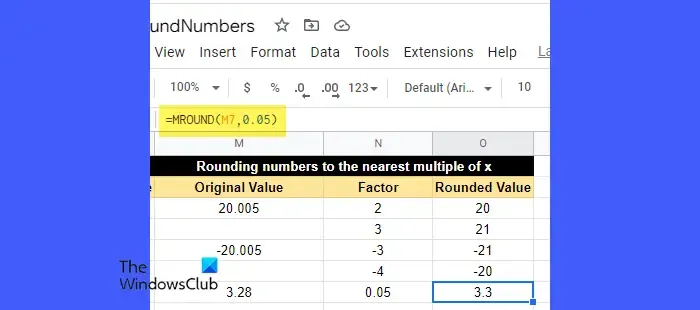
MROUND 函數的語法是:
MROUND(value,factor)
- 其中value是需要四捨五入的數字,並且
- factor是其倍數成為給定數字應四捨五入的最接近數字的數字。
- 使用 MROUND 函數時,只有當值參數也為負時,您才能在因子參數中傳遞負值。
- 值和因子參數都可以是非整數的。
- 如果在 factor 參數中傳遞 0,MROUND 函數將返回 0。
- 如果 factor 的 2 個倍數與該值同樣最接近,則返回絕對值較高的倍數。
要理解這一點,請查看上圖。單元格 M7 (3.28) 中的值已四捨五入為 3.3。此處,因子值為 0.05。如果我們繼續將該因子與 1、2、3 等相乘,我們將找到以下最接近 3.28 的數字:
0.05 x 64 = 3.2
0.05 x 65 = 3.25
0.05 x 66 = 3.3
0.05x 67 = 3.35
在所有這些中,最接近的是 3.3。因此 MROUND 函數返回了 3.3 作為結果。
5] 使用 INT 函數舍入數字
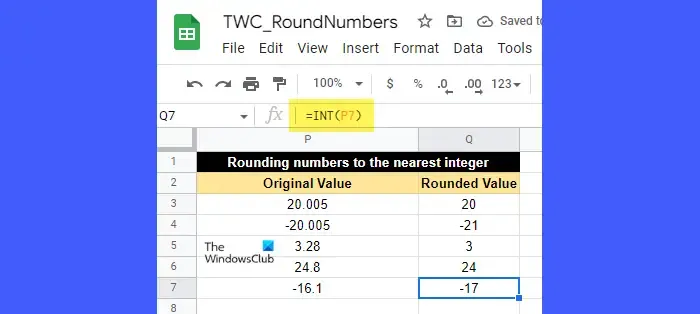
INT函數用於向下舍入小數。它總是將數字向下舍入到小於或等於它的最接近的整數。
INT函數的語法是:
INT(value)
- 其中value是需要四捨五入的數字。
要理解這一點,請查看上圖。單元格 P6 (24.8) 中的值已四捨五入為 24,這是小於 24.8 的最接近的整數。同樣,單元格 P7 (-16.1) 中的值已四捨五入為 -17,這是小於 -16.1 的最接近整數。
INT 函數和 ROUNDDOWN 函數之間的主要區別在於 INT 函數向下舍入給定數字的值,而 ROUNDDOWN 函數向下舍入給定數字的“絕對”值。因此,如果我們將 ROUNDDOWN 函數應用於單元格 P7,結果將為 -16,而不是 -17。
6] 使用 FLOOR 函數對數字進行舍入
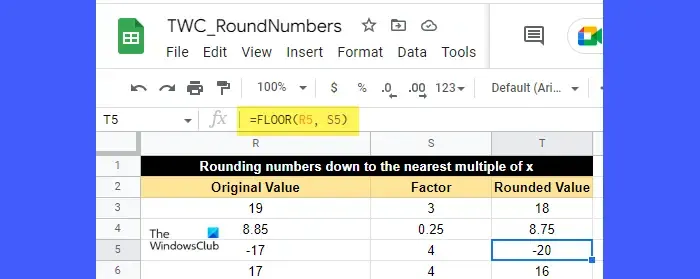
FLOOR 函數的語法是:
FLOOR(value, [factor])
- 其中value是需要四捨五入的數字,並且
- factor是數字(僅正數),其倍數是值應四捨五入到的最接近的數字。它是一個可選參數,默認值為 1。
要了解 FLOOR 函數,請查看上圖。單元格 R5 (-17) 中的值已向下舍入為 -20,即 4 的倍數,最接近 -17。同樣,單元格 R3 (19) 中的值已向下舍入為 18,這是最接近 19 的 3 的倍數。
7] 使用 CEILING 函數的捨入數
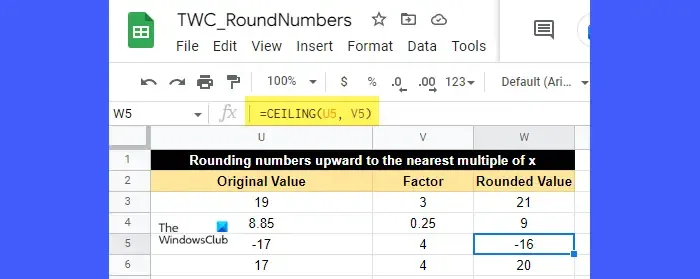
CEILING 函數的語法是:
CEILING(value, [factor])
- 其中value是需要四捨五入的數字,並且
- factor是數字(正數或負數),其倍數是值應四捨五入到的最接近的數字。它是一個可選參數,如果用戶未指定,則取值 1。
如果值為正,則因子也必須為正。但是,如果該值為負數,則該因子可能為正數或負數,以確定值應按哪個方向四捨五入。
例如,請看上圖。單元格 U5 (-17) 中的值已向上舍入為 -16,這是最接近 -17 的 4 的倍數。同樣,單元格 U3 (19) 中的值已向上舍入為 21,這是最接近 19 的 3 的倍數。
所以這結束了你如何在谷歌表格中舍入數字。希望你覺得這個有用。



發佈留言